Moving average

Assessment | Biopsychology | Comparative | Cognitive | Developmental | Language | Individual differences | Personality | Philosophy | Social |
Methods | Statistics | Clinical | Educational | Industrial | Professional items | World psychology |

Statistics: Scientific method · Research methods · Experimental design · Undergraduate statistics courses · Statistical tests · Game theory · Decision theory

---

In statistics, a moving average is one of a family of similar techniques used to analyze time series data. A moving average series can be calculated for any time series. Moving averages are used to smooth out short-term fluctuations, thus highlighting longer-term trends or cycles. The threshold between short-term and long-term depends on the application, and the parameters of the moving average will be set accordingly.

Mathematically, each of these moving averages is an example of a convolution. These averages are also similar to the low-pass filters used in signal processing.

Simple moving average

A simple moving average (SMA) is the unweighted mean of the previous n data points. For example, a 10-day simple moving average of closing price is the mean of the previous 10 days' closing prices. If those prices are $p_{M}$, $p_{M-1}$... $p_{M-9}$ then the formula is

$\textit{SMA} = { p_{M} + p_{M-1} + \cdots + p_{M-9} \over 10 }$

When calculating successive values, a new value comes into the sum and an old value drops out, meaning a full summation each time is unnecessary,

$\textit{SMA}_\mathrm{today} = \textit{SMA}_\mathrm{yesterday} - {p_{M-n+1} \over n} + {p_{M+1} \over n}$

In technical analysis there are various popular values for n, like 10 days, 40 days, or 200 days. The period selected depends on the kind of movement one is concentrating on, such as short, intermediate, or long term. In any case moving average levels are interpreted as support in a rising market, or resistance in a falling market.

In all cases a moving average lags behind the latest price action, simply from the nature of its smoothing. An SMA can lag to an undesirable extent, and can be influenced too much by old prices dropping out of the average. This is addressed by giving extra weight to recent prices, as in the WMA and EMA below.

One characteristic of the SMA is that if the data has a periodic fluctuation, then applying an SMA of that period will eliminate that variation (the average always containing one complete cycle). But a perfectly regular cycle is rarely encountered in economics or finance.

Weighted moving average

A weighted average is any average that has multiplying factors to give different weights to different data points. But in technical analysis a weighted moving average (WMA) has the specific meaning of weights which decrease arithmetically. In an n-day WMA the latest day has weight n, the second latest n-1, etc, down to zero.

$\textit{WMA}_{M} = { n p_{M} + (n-1) p_{M-1} + \cdots + 2 p_{M-n+2} + p_{M-n+1} \over n + (n-1) + \cdots + 2 + 1}$

When calculating the WMA across successive values, it can be noted the difference between the numerators of $WMA_{M+1}$ and $WMA_{M}$ is $n p_{M+1} - p_{M} - \cdots - p_{M-n+1}$. If we denote the sum $p_{M} + \cdots + p_{M-n+1}$ by $Total_{M}$, then

$Total_{M+1} = Total_{M} + p_{M+1} - p_{M-n+1}$

$\textit{Numerator}_{M+1} = \textit{Numerator}_{M} + n p_{M+1} - Total_{M}$

$\textit{WMA}_{M+1} = { \textit{Numerator}_{M+1} \over n + (n-1) + \cdots + 2 + 1}$

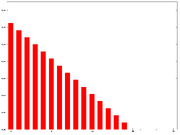
WMA weights n=15

The denominator is a triangle number, and can be easily computed as $n(n+1)\over2$

The graph at the right shows how the weights decrease, from highest weight for the most recent days, down to zero. It can be compared to the weights in the exponential moving average which follows.

Exponential moving average

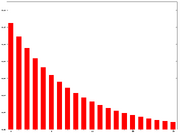
EMA weights N=15

An exponential moving average (EMA), sometimes also called an exponentially weighted moving average (EWMA), applies weighting factors which decrease exponentially. The weighting for each day decreases exponentially, giving much more importance to recent observations while still not discarding older observations entirely. The graph at right shows an example of the weight decrease.

The degree of weighing decrease is expressed as a constant smoothing factor α, a number between 0 and 1. α may be expressed as a percentage, so a smoothing factor of 10% is equivalent to α=0.1. Alternately, α may be expressed in terms of N time periods, where $\alpha={2\over{N+1}}$. For example, N=19 is equivalent to α=0.1.

The observation at a time period t is designated Y_t, and the value of the EMA at any time period t is designated S_t. S₁ is undefined. S₂ may be initialized in a number of different ways, most commonly by setting S₂ to Y₁, though other techniques exist, such as setting S₂ to an average of the first 4 or 5 observations. The prominence of the S₂ initialization's effect on the resultant moving average depends on α; smaller α values make the choice of S₂ relatively more important than larger α values, since a higher α discounts older observations faster.

The formula for calculating the EMA at time periods t≥2 is

$S_{t} = \alpha \times Y_{t-1} + (1-\alpha) \times S_{t-1}$

This formulation is according to Hunter (1986); an alternate approach by Roberts (1959) uses Y_t in place of Y_t-1

This formula can also be expressed in technical analysis terms as follows, showing how the EMA steps towards the latest price, but only by a proportion of the difference (each time),

$\textit{EMA}_{\text{today}} = \textit{EMA}_{\text{yesterday}} + \alpha \times (\textit{price} - \textit{EMA}_{\text{yesterday}})$

Expanding out $\textit{EMA}_{\textit{yesterday}}$ each time results in the following power series, showing how the weighting factor on each price $p_1$, $p_2$, etc, decrease exponentially,

$\textit{EMA} = { p_1 + (1-\alpha) p_2 + (1-\alpha)^2 p_3 + (1-\alpha)^3 p_4 + \cdots \over 1 + (1-\alpha) + (1-\alpha)^2 + (1-\alpha)^3 + \cdots }$

In theory this is an finite sum, but because 1-α is less than 1, the terms become smaller and smaller, and can be ignored once small enough. The denominator approaches 1/α, and that value can be used instead of adding up the powers, provided one is using enough terms that the omitted portion is negligible.

The N periods in an N-day EMA only specifies the α factor. It isn't a stopping point for the calculation in the way N is in an SMA or WMA. The first N days in an EMA do represent about 86% of the total weight in the calculation though.

The power formula above gives a starting value for a particular day, after which the successive days formula shown first can be applied.

The question of how far back to go for an initial value depends, in the worst case, on the data. If there are huge p price values in old data then they'll have an effect on the total even if their weighting is very small. If one assumes prices don't vary too wildly then just the weighting can be considered, and work out how much weight is omitted by stopping after say k terms. This is $(1-\alpha)^k + (1-\alpha)^{k+1} + \cdots$, which is $(1-\alpha)^k \times (1 + (1-\alpha) + (1-\alpha)^2 \cdots)$, ie. a fraction ${(1-\alpha)^k \over \alpha}$ out of the total weight.

Thus if the aim was to have 99.9% of the weight then $k={ \log (0.001 \times \alpha) \over \log (1-\alpha)}$ many terms should be used. And what's more it can be shown $\log\,(1-\alpha)$ approaches $-2 \over N+1$ as N increases, so this simplifies to (roughly) $k=3.45\times(N+1)$ for this example 99.9% weight.

J. Welles Wilder

Noted technical analyst J. Welles Wilder uses a different form for specifying the period of an EMA. For say 14 days he writes

$\textit{EMA}_{\text{today}} = {1\over14} \times \text{price} + {13\over14} \times \textit{EMA}_{\text{yesterday}}$

So α=1/N rather than α=2/(N+1) as described above. The calculation and properties are all the same, it's just a different reckoning of the rate of smoothing. Clearly care must be taken with which is intended. A conversion can be easily made, for instance 14-days from Wilder is equivalent to 27-days in the above (conversion 2N-1).

Other weightings

Other weighting systems are used occasionally – for example, a volume weighting will weight each time period in proportion to its trading volume.

There are weighting systems designed using a combination of moving averages: The DEMA indicator (and TEMA indicator (Triple Exponential Moving Average) are unique composites of a single exponential moving average, a double exponential moving average, and in the latter case a triple exponential moving average that provides less lag than either of the three components individually. They were originally introduced January 1994 by Patrick Mulloy.^{[How to reference and link to summary or text]}

The TRIX indicator uses a triple-EMA in its calculation. This ends up as just a certain set of weights on past data, and a set quite different from a plain EMA actually.

See also

• Exponential smoothing

External links

• Moving Average Code Implementation